虚功原理
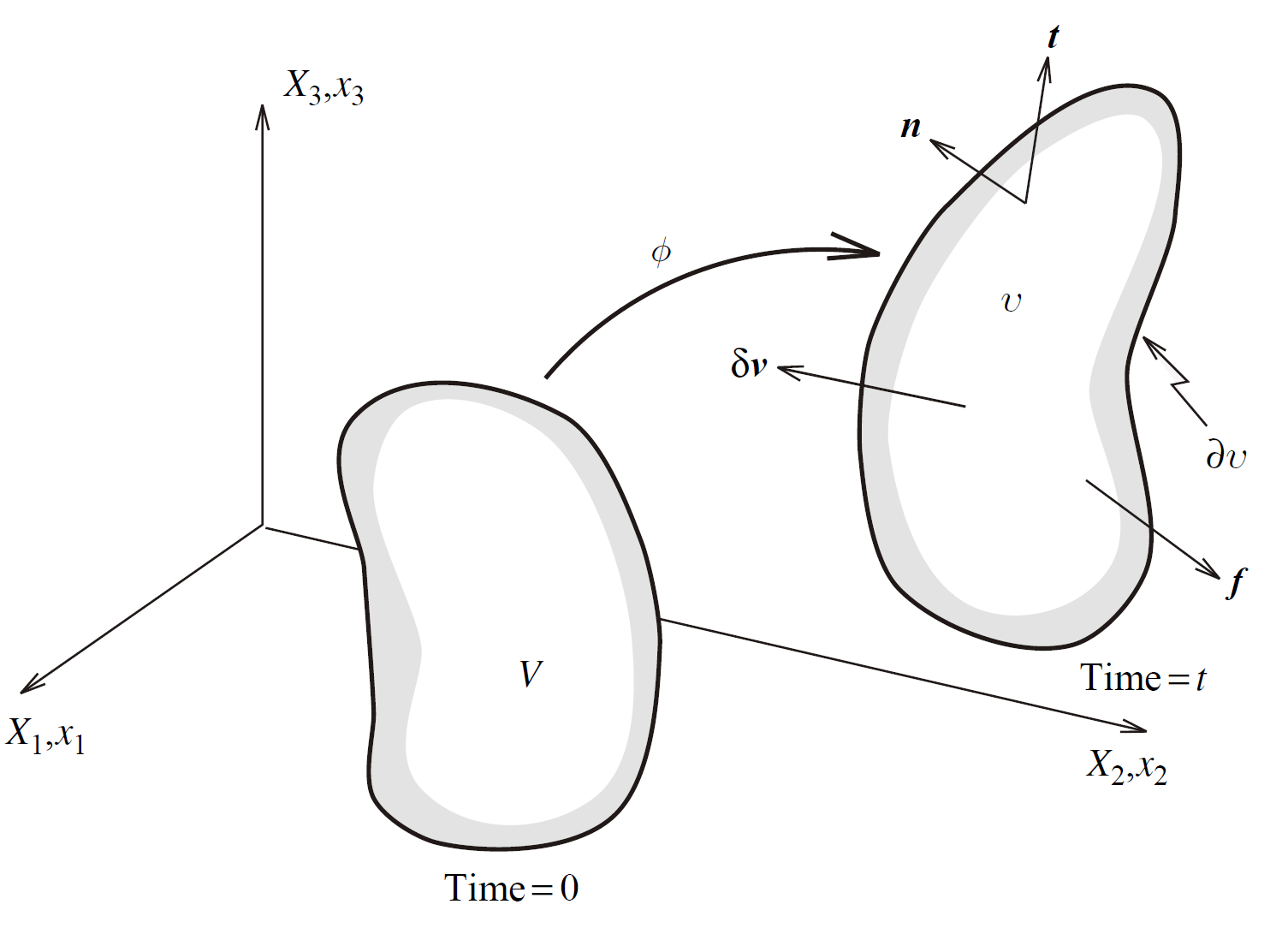
- $\delta \boldsymbol{v}$ 虚速度(virtual velocity)
- $\boldsymbol{r}$ 残余力(residual force)
- $\delta \boldsymbol{l}$ 虚速度梯度 the virtual velocity gradient
- $\boldsymbol{t}$ traction vector
虚功(virtual work): $\delta w$, 单位体积单位时间内,虚运动过程中残余力(residual force)的做功为零。
$$ \delta w=\boldsymbol{r}\cdot\delta\boldsymbol{v}=0 $$由于$\delta \boldsymbol{v}$ 的任意性,上述式子等价于$\boldsymbol{r}=0$
物体的静态平衡方程的弱形式为
$$ \delta W=\int_v(\operatorname{div} \boldsymbol{\sigma}+\boldsymbol{f}) \cdot \delta \boldsymbol{v} d v=0 $$根据 $\text{div}$ 算子的性质
$$ \operatorname{div}(\boldsymbol{\sigma} \delta \boldsymbol{v})=(\operatorname{div} \boldsymbol{\sigma}) \cdot \delta \boldsymbol{v}+\boldsymbol{\sigma}: \boldsymbol{\nabla} \delta \boldsymbol{v} $$以及高斯定理, 可以得到
$$ \int_{\partial v} \boldsymbol{n} \cdot \boldsymbol{\sigma} \delta \boldsymbol{v} d a-\int_v \boldsymbol{\sigma}: \boldsymbol{\nabla} \delta \boldsymbol{v} d v+\int_v \boldsymbol{f} \cdot \delta \boldsymbol{v} d v=0 $$$$ \boldsymbol{t}(\boldsymbol{n})=\boldsymbol{\sigma} \boldsymbol{n} ; \quad \boldsymbol{\sigma}=\sum_{i, j=1}^3 \sigma_{i j} \boldsymbol{e}_i \otimes \boldsymbol{e}_j $$可以得到
$$ \int_v \boldsymbol{\sigma}: \delta \boldsymbol{l} d v=\int_v \boldsymbol{f} \cdot \delta \boldsymbol{v} d v+\int_{\partial v} \boldsymbol{t} \cdot \delta \boldsymbol{v} d a $$$\delta \boldsymbol{l}$ 可以拆分成 $\delta \boldsymbol{d}$ 对称虚形变变化率,$\delta \boldsymbol{w}$ 反对称虚旋转张量,考虑到$\boldsymbol{\sigma}$的对称性,上述方程可以写成
$$ \delta W=\int_v \boldsymbol{\sigma}: \delta \boldsymbol{d} d v-\int_v \boldsymbol{f} \cdot \delta \boldsymbol{v} d v-\int_{\partial v} \boldsymbol{t} \cdot \delta \boldsymbol{v} d a=0 $$spatial virtual work equation,是一个标量方程,描述了形变物体的平衡状态,有限元离散的基础。
功的共轭性
虚内功(virtual internal work)
$$ \begin{equation} \delta W_{\mathrm{int}}=\int_v \boldsymbol{\sigma}: \delta \boldsymbol{d} d v \end{equation} $$$\boldsymbol{\sigma}$ 和 $\boldsymbol{d}$ 是共轭(work conjugate)的,关于当前形变体积,它们的内积得到单位当前体积做的功。
material coordinate
$\boldsymbol{\tau}$ Kirchhoff stress tensor ,与$\boldsymbol{d}$ 是共轭的,关于初始位移,
$$ \begin{equation} \delta W_{\mathrm{int}}=\int_V \boldsymbol{\tau}: \delta \boldsymbol{d} d V ; \quad \boldsymbol{\tau}=J \boldsymbol{\sigma} \end{equation} $$P first Piola–Kirchhoff stress tensor, 与形变梯度的变化率共轭
$$ \begin{equation} \begin{aligned} \delta W_{\mathrm{int}} & =\int_V J \boldsymbol{\sigma}: \delta \boldsymbol{l} d V \\ & =\int_V J \boldsymbol{\sigma}:\left(\delta \dot{\boldsymbol{F}} \boldsymbol{F}^{-1}\right) d V \\ & =\int_V \operatorname{tr}\left(J \boldsymbol{F}^{-1} \boldsymbol{\sigma} \delta \dot{\boldsymbol{F}}\right) d V \\ & =\int_V\left(J \boldsymbol{\sigma} \boldsymbol{F}^{-T}\right): \delta \dot{\boldsymbol{F}} d V \end{aligned} \end{equation} $$这两者在虚功的意义下是相等的。
$$ -\frac{\partial \Psi}{\partial \boldsymbol{X}}\cdot \delta\boldsymbol{v} $$$$ F = \nabla\cdot\mathbb{P}? $$$$ \boldsymbol{F}=-\frac{\partial \Psi(\mathbb{F}(\boldsymbol{X}),\boldsymbol{X})}{\partial \boldsymbol{X}}=-\frac{\partial \Psi}{\partial \mathbb{F}}\frac{\partial \mathbb{F}}{\partial \boldsymbol{X}}=-\mathbb{P}\frac{\partial F}{\partial \boldsymbol{X}} $$Kirchhoff 应力张量
称 $\sigma$ 和 $\boldsymbol{d}$ 为work conjugate
该方程中的σ和d等对被称为与电流变形体积的功共轭,因为它们的乘积给出了单位电流体积的功。
hugo new –kind post-bundle post/virtual-work-principle
达朗贝尔原理
(D’Alembert’s principle)
总势能函数和平衡状态
总势能泛函为:
$$ \Pi(\boldsymbol{\phi})=\int_V \Psi(\boldsymbol{C}) d V-\int_V \boldsymbol{f}_0 \cdot \boldsymbol{\phi} d V-\int_{\partial V} \boldsymbol{t}_0 \cdot \boldsymbol{\phi} d A , $$其方向导数产生虚功原理
$$ \begin{aligned} D \Pi(\phi)[\delta \boldsymbol{v}] & =\int_V \frac{\partial \Psi}{\partial \boldsymbol{C}}: D \boldsymbol{C}[\delta \boldsymbol{v}] d V-\int_V \boldsymbol{f}_0 \cdot \delta \boldsymbol{v} d V-\int_{\partial V} \boldsymbol{t}_0 \cdot \delta \boldsymbol{v} d A \\ & =\int_V \boldsymbol{S}: D \boldsymbol{E}[\delta \boldsymbol{v}] d V-\int_V \boldsymbol{f}_0 \cdot \delta \boldsymbol{v} d V-\int_{\partial V} \boldsymbol{t}_0 \cdot \delta \boldsymbol{v} d A=0 \end{aligned} $$(p. 225.):